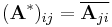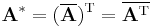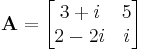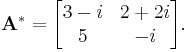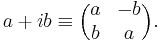Conjugate transpose

In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A^* obtained from A by taking the transpose and then taking the complex conjugate of each entry (i.e., negating their imaginary parts but not their real parts). The conjugate transpose is formally defined by

$(\mathbf{A}^*)_{ij} = \overline{\mathbf{A}_{ji}}$

where the subscripts denote the i,j-th entry, for 1 ≤ i ≤ n and 1 ≤ j ≤ m, and the overbar denotes a scalar complex conjugate. (The complex conjugate of 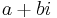$a %2B bi$ , where a and b are reals, is $a - bi$ .)

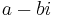This definition can also be written as

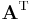$\mathbf{A}^* = (\overline{\mathbf{A}})^\mathrm{T} = \overline{\mathbf{A}^\mathrm{T}}$

where $\mathbf{A}^\mathrm{T} \,\!$ denotes the transpose and 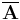$\overline{\mathbf{A}} \,\!$ denotes the matrix with complex conjugated entries.

Other names for the conjugate transpose of a matrix are Hermitian conjugate, or transjugate. The conjugate transpose of a matrix A can be denoted by any of these symbols:

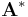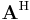$\mathbf{A}^* \,\!$ or $\mathbf{A}^\mathrm{H} \,\!$ , commonly used in linear algebra
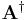$\mathbf{A}^\dagger \,\!$ (sometimes pronounced "A dagger"), universally used in quantum mechanics
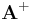$\mathbf{A}^%2B \,\!$ , although this symbol is more commonly used for the Moore-Penrose pseudoinverse

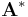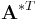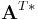In some contexts, $\mathbf{A}^* \,\!$ denotes the matrix with complex conjugated entries, and thus the conjugate transpose is denoted by $\mathbf{A}^{*T} \,\!$ or $\mathbf{A}^{T*} \,\!$ .

1 Example
2 Basic remarks
3 Motivation
4 Properties of the conjugate transpose
5 Generalizations
6 See also
7 External links

Example

$\mathbf{A} = \begin{bmatrix} 3 %2B i & 5 \\ 2-2i & i \end{bmatrix}$

then

$\mathbf{A}^* = \begin{bmatrix} 3-i & 2%2B2i \\ 5 & -i \end{bmatrix}.$

Basic remarks

A square matrix A with entries 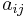$a_{ij}$ is called

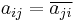Hermitian or self-adjoint if A = A^*, i.e., $a_{ij}=\overline{a_{ji}}$ .
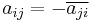skew Hermitian or antihermitian if A = −A^*, i.e., $a_{ij}=-\overline{a_{ji}}$ .
normal if A^*A = AA^*.
unitary if A^* = A^-1.

Even if A is not square, the two matrices A^*A and AA^* are both Hermitian and in fact positive semi-definite matrices.

The adjoint matrix A^* should not be confused with the adjugate adj(A) (which is also sometimes called "adjoint").

Motivation

The conjugate transpose can be motivated by noting that complex numbers can be usefully represented by 2×2 real matrices, obeying matrix addition and multiplication:

$a %2B ib \equiv \Big(\begin{matrix} a & -b \\ b & a \end{matrix}\Big).$

That is, denoting each complex number z by the real 2×2 matrix of the linear transformation on the Argand diagram (viewed as the real vector space 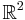$\mathbb{R}^2$ ) affected by complex z-multiplication on $\mathbb{C}$ .

An m-by-n matrix of complex numbers could therefore equally well be represented by a 2m-by-2n matrix of real numbers. The conjugate transpose therefore arises very naturally as the result of simply transposing such a matrix, when viewed back again as n-by-m matrix made up of complex numbers.

Properties of the conjugate transpose

(A + B)^* = A^* + B^* for any two matrices A and B of the same dimensions.
(r A)^* = r^*A^* for any complex number r and any matrix A. Here r^* refers to the complex conjugate of r.
(AB)^* = B^*A^* for any m-by-n matrix A and any n-by-p matrix B. Note that the order of the factors is reversed.
(A^*)^* = A for any matrix A.
If A is a square matrix, then det(A^*) = (det A)^* and tr(A^*) = (tr A)^*
A is invertible if and only if A^* is invertible, and in that case we have (A^*)⁻¹ = (A⁻¹)^*.
The eigenvalues of A^* are the complex conjugates of the eigenvalues of A.
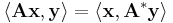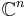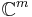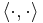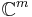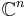$\langle \mathbf{Ax}, \mathbf{y}\rangle = \langle \mathbf{x},\mathbf{A}^* \mathbf{y} \rangle$ for any m-by-n matrix A, any vector x in $\mathbb{C}^n$ and any vector y in $\mathbb{C}^m$ . Here $\langle\cdot,\cdot\rangle$ denotes the standard complex inner product on $\mathbb{C}^m$ and $\mathbb{C}^n$ .

Generalizations

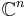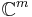The last property given above shows that if one views A as a linear transformation from the Euclidean Hilbert space $\mathbb{C}^n$ to $\mathbb{C}^m$ , then the matrix A^* corresponds to the adjoint operator of A. The concept of adjoint operators between Hilbert spaces can thus be seen as a generalization of the conjugate transpose of matrices.

Another generalization is available: suppose A is a linear map from a complex vector space V to another W, then the complex conjugate linear map as well as the transposed linear map are defined, and we may thus take the conjugate transpose of A to be the complex conjugate of the transpose of A. It maps the conjugate dual of W to the conjugate dual of V.

External links

Weisstein, Eric W., "Conjugate Transpose" from MathWorld.
Conjugate transpose on PlanetMath